Лекция 1. Введение
Copyright © Красноярский государственный университет 2003
Содержание
Общие принципы работы с пакетом Matlab
Переменные и знаки операций
Функции в Matlab
Как передать в Matlab данные из других программ
О рациональной технике программирования в Matlab
Список наиболее часто употребляемых функций пакета Matlab
Элементарные функции
Специальные функции
Функции для работы с матрицами
Функции для численного анализа
Задачи
Общие принципы работы с пакетом Matlab
Matlab - интепретатор , что означает последовательное выполнение вводимых операторов
без предварительной компиляции. Matlab имеет собственную оболочку и язык для разработки и
выполнения программ. Общий вид среды разработки показан на рис. 1.1.
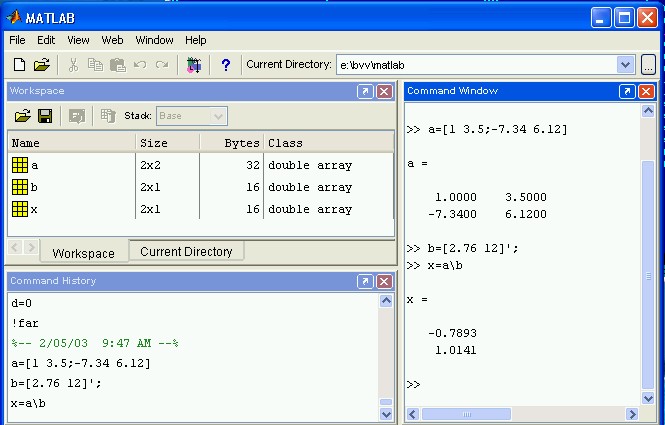 Рис. 1.1 Среда разработки Matlab
По умолчанию открыто три окна. Окно Command Window предназначено для ввода команд,
в окне Workspace отображаются переменные , храняшиеся в памяти. Окно Command History
протоколирует вводимые команды. Операторы Matlab могут вводиться в командном окне
или из файлов с именами *.m (звездочка обозначает произвольное имя).
Например, если в директории е:\bvv\matlab имеется файл
name.m c набором операторов Matlab, то для его выполнения необходимо
выполнить следующие действия.
1. Ввести в командном окне Matlab команду path(path,'e:\bvv\matlab'); .
Эта команда добавляет к пути поиска m-файлов путь e:\bvv\matlab.
2. После добавления пути к переменной path можно запускать программу, набрав в командном
окне name (без .m).
При вводе команды name Matlab выполняет следующие действия.
1. Просматривает список переменных в памяти и, если в памяти хранится переменная
с именем name, ее значение выводится на экран.
2. Если переменнная с именем name не найдена, далее просматриваются все файлы в текущей
директории. Текущая директория определена в окне Current Directory среды разработки.
Сменить текущую директорию можно командой cd. Например, cd e:\bvv\matlab. Вывести текущую
директорию на экран можно командой pwd.
Если файл name.m найден, он запускается на выполнение.
3. Если в текущей директории файл name.m не обнаружен, тогда просматриваются все пути
из переменной path и первый найденный файл name.m запускается на выполнение.
Следует обратить особое внимание на имена создаваемых m-файлов. Дело в том, что в Matlab
в директории %MATLAB\toolbox (%MATLAB - путь к директории, где инсталлирован Matlab)
содержится очень большое количество файлов с именами *.m, а пути на все поддиректории
директории toolbox содержатся в переменной path. Команда path(path,'e:\bvv\matlab')
добавляет путь e:\bvv\matlab в конец переменной path, поэтому возникает опасность
дублирования имен, а я уже отмечал, что Matlab запускает на исполнение первый найденный
файл. Можно добавлять свой путь поиска в начало или в конец переменной path командой
addpath. Например, чтобы добавить путь e:\bvv\matlab в начало переменной path нужно
ввести команду addpath e:\bvv\matlab -begin, а команда addpath e:\bvv\matlab -end
поставит этот путь в конец переменной path.
Удалить путь из переменнной path можно командой rmpath e:\bvv\matlab.
В любой момент можноь получить справку о любой функции matlab с помощью команды
help. Например, чтобы получить информацию о синтаксисе команды addpath, необходимо
ввести команду help addpath. Получить список переменных, хранящихся в памяти, позволяет
команда whos (или ее короткая форма who). Удалить переменную var из памяти можно
командой clear var, а удалить все переменные из памяти clear all.
Команда format управляет форматом вывода переменных на консоль.
Рис. 1.1 Среда разработки Matlab
По умолчанию открыто три окна. Окно Command Window предназначено для ввода команд,
в окне Workspace отображаются переменные , храняшиеся в памяти. Окно Command History
протоколирует вводимые команды. Операторы Matlab могут вводиться в командном окне
или из файлов с именами *.m (звездочка обозначает произвольное имя).
Например, если в директории е:\bvv\matlab имеется файл
name.m c набором операторов Matlab, то для его выполнения необходимо
выполнить следующие действия.
1. Ввести в командном окне Matlab команду path(path,'e:\bvv\matlab'); .
Эта команда добавляет к пути поиска m-файлов путь e:\bvv\matlab.
2. После добавления пути к переменной path можно запускать программу, набрав в командном
окне name (без .m).
При вводе команды name Matlab выполняет следующие действия.
1. Просматривает список переменных в памяти и, если в памяти хранится переменная
с именем name, ее значение выводится на экран.
2. Если переменнная с именем name не найдена, далее просматриваются все файлы в текущей
директории. Текущая директория определена в окне Current Directory среды разработки.
Сменить текущую директорию можно командой cd. Например, cd e:\bvv\matlab. Вывести текущую
директорию на экран можно командой pwd.
Если файл name.m найден, он запускается на выполнение.
3. Если в текущей директории файл name.m не обнаружен, тогда просматриваются все пути
из переменной path и первый найденный файл name.m запускается на выполнение.
Следует обратить особое внимание на имена создаваемых m-файлов. Дело в том, что в Matlab
в директории %MATLAB\toolbox (%MATLAB - путь к директории, где инсталлирован Matlab)
содержится очень большое количество файлов с именами *.m, а пути на все поддиректории
директории toolbox содержатся в переменной path. Команда path(path,'e:\bvv\matlab')
добавляет путь e:\bvv\matlab в конец переменной path, поэтому возникает опасность
дублирования имен, а я уже отмечал, что Matlab запускает на исполнение первый найденный
файл. Можно добавлять свой путь поиска в начало или в конец переменной path командой
addpath. Например, чтобы добавить путь e:\bvv\matlab в начало переменной path нужно
ввести команду addpath e:\bvv\matlab -begin, а команда addpath e:\bvv\matlab -end
поставит этот путь в конец переменной path.
Удалить путь из переменнной path можно командой rmpath e:\bvv\matlab.
В любой момент можноь получить справку о любой функции matlab с помощью команды
help. Например, чтобы получить информацию о синтаксисе команды addpath, необходимо
ввести команду help addpath. Получить список переменных, хранящихся в памяти, позволяет
команда whos (или ее короткая форма who). Удалить переменную var из памяти можно
командой clear var, а удалить все переменные из памяти clear all.
Команда format управляет форматом вывода переменных на консоль.
Переменные и знаки операций
Переменные в Matlab не объявляются, как в других языках программирования, а вводятся
по ходу выполнения программы. По умолчанию все переменные являются матрицами из вещественных
чисел типа double (аналог типа double в Си). Например, ввести матрицу 2x2 можно командой
a=[1 3.5;-7.34 6.12], как показано на рис. 1.1. Если после введенной команды не поставить
точку с запятой ;, то результат выводится на консоль. На рис. 1.1 введены две матрицы a -
размером 2x2 и b - 2x1. Далее показано как c помощью знака операции \ (обратная косая)
решить систему линейных уравнений, определенных матрицей a и вектором правых частей b.
Решение помещается в переменную x и выводится на консоль. Можно проверить, что x
действительно решение командой a*x-b - на консоли увидите переменную ans 2x1 c нулевыми
элементами. По умолчанию результат помещается в переменную с именем ans.
Обращаются к матричным элементам с помощью круглых скобок, а индексы нумеруются
с единицы (как в фортране). Например a(2,1) - матричный элемент из второй строки и первого
столбца. Вводимые матрицы могут быть комплексными, для обозначения мнимой единицы
зарезервированы две переменнные - i и j. Однако по ходу выполнения программы эти переменные
могут быть переопределены. Вот пример ввода комплексной матрицы
ac=[1+2*i 4*i;3.6 -7.35+3.67*i]. Приведу несколько функций для генерирования матриц:
a1=ones(5,5) - матрица 5x5 с единичными матричными элементами,
a2=zeros(4,6) - матрица 4x6 c нулевыми матричными элементами,
a3=eye(4,4) - единичная матрица 4x4,
a4=rand(7,8) - 7x8 матрица со случайными матричными элементами из интервала [0-1].
Размерность массивов в matlab произвольная, т.е. можно заводить массивы 3-x мерные,
4-x мерные и т.д. Очень часто при оперировании с массивами используется символ :.
Например, c=a(:,1); - в переменную с занесены все строки первого столбца матрицы a,
или c1=a(2:4,2); - в c1 занесены строки со второй по четвертую второго столбца матрицы a.
C помощью оператора x=0:0.1:2*pi; (pi предопределенная переменная)
заводится новая переменная-строка, элементами которой являются все значения от нуля до 2*pi
с шагом 0.1.
В matlab определены следующие знаки арифметических операций:
+ сложение,
- вычитание,
* матричное умножение,
/ матричное деление,
\ обратное деление,
^ возведение в степень,
' транспонирование
.* поэлементное умножение,
./ поэлемнтное деление,
.\ обратное поэлементное деление,
.^ поэлементное возведение в степень
.' поэлементное транспонирование.
Описание знаков операций.
+ Сложение или унарный плюс. При сложении матрицы должны иметь одинаковые размеры.
К матрице любого размера можно прибавлять скаляр.
- Вычитание или унарный минус. При вычитании матрицы должны иметь одинаковые размеры.
Из матрицы любого размера можно вычитать скаляр.
* Матричное умножение. Сомножители должны иметь правильные размеры.
/ Деление матриц. A/B эквивалентно A*inv(B), inv - функция для вычисления обратной матрицы.
^ В выражении C^p p должно быть скаляром. Если p целое, тогда C перемножается p раз.
Если p отрицательное, то от C берется обратная матрица. Если p вещественное, тогда
сначала вычисляются собственные значения и собственные вектора матрицы C
[V,D]=eig(C);, где V - матрица, содержащая в столбцах собственные вектора матрицы C,
а D - диагональная матрица с собственными значениями C на диагонали.
Результат возведения в степень вычисляется так C^p=V*D.^p/V. Описание операции .^
приведено ниже.
\ Левое деление. A\B эквивалентно inv(A)*B. Если A квадратная матрица nxn, а B вектор
столбец из n элементов, или матрица из нескольких столбцов по n элементов, тогда
результатом операции A\B является решение системы линейных уравнений A*X=B.
' Транспонирование матриц. Если матрица комплексная, то выполняется транспонирование и
комплексное сопряжение.
.* Поэлементное умножение. y=x.*z; означает, что y(i,j)= x(i,j)*z(i,j). Матрицы x,z и y должны
иметь одинаковые размеры.
./ Поэлементное деление. y=x./z; означает, что y(i,j) = x(i,j)/z(i,j).
Матрицы x и z должны быть одинаковых размеров.
.^ y=x.^z; означает, что y(i,j)=x(i,j)^z(i,j). Матрицы x и z должны быть одинаковых размеров.
.' r=y.'; означает, что r(i,j)=1/y(i,j).
.\ C=A.\B; означает, что C(i,j)=B(i,j)/A(i,j).
В качестве примера применения поэлементных операций решим такую задачу. Требуется построить
график функции y(x)=e -x2cos(x) для x из интервала [0 2*pi].
Вот решение: (файл l1_1.m )
x=0:2*pi/50:2*pi; % x вектор-строка из 51 элемента
y=exp(-x.^2).*cos(x); % y вектор-строка из 51 элемента y(i)=exp(-x(i)^2)*cos(x(i))
plot(x,y); % рисуем график
В файлах *.m символ % используется для комментария до конца строки.
Во второй строке скрипта x.^2 - матрица из одной строки и 51 столбца со значениями
x(1)2, x(2)2, x(3)2 и т.д.
exp(-x.^2) - матрица из одной строки и 51 столбца с элементами
e(-x(1)2) , e(-x(2)2) ... e(-x(51)2).
В переменной y хранится матрица из одной строки и 51 столбца с элементами
e(-x(1)2)cos(x(1)), e(-x(2)2)cos(x(2)), ...
e(-x(51)2)cos(x(51)).
Функция plot строит двумерый график. Для построения трехмерных графиков используется
функция plot3. Например, построим график пространственной спирали
(файл l1_2.m ).
t=0:pi/100:6*pi;
x=cos(t);
y=sin(t);
plot3(x,y,t);
В matlab определены операции сравнения <, >, <=, >=, ==, ~= (не равно).
Матрицы в операциях сравнения должны иметь одинаковые размеры. Все операции сравнения
производят поэлементное сравнение матричных элементов. Результатом операции
сравнения является матрица из нулей и единиц и того же размера, что и сравниваемые матрицы.
Синтаксис для логических операций
A&B логическое И,
A|B логическое OR (включающее ИЛИ),
xor(A,B) логическое XOR (исключающее ИЛИ),
~A логическое отрицание.
Операнды логических операций должны иметь одинаковые размеры. Логические операции производят
поэлементные операции над матричными элементами. Результатом логической операции
всегда является матроица из нулей и единиц и того же размера, что и операнды.
Например,
A B A&B A|B xor(A,B) ~A
0 0 0 0 0 1
1 0 0 1 1 0
0 1 0 1 1 1
1 1 1 1 0 0 .
Функции в Matlab
Функуции в Matlab пишутся в отдельных файлах. Один файл может содержать описание
только одной функции. Имя файла должно совпадать с именем функции, которая в этом файле
описана. Все имена файлов с функциями имеют расширение .m. В качестве примера
приведу содержимое файла myfunc.m , содержащего описание функции
одного переменного и возвращающей одно значение.
function y=myfunc(x)
global alpha
y=sin(alpha*x.^2).*cos(x);
Во второй строке объявляется глобальная переменная alpha. Все переменные в функциях Matlab
являются локальными, т.е. видны только в пределах функции. Если Вы хотите, чтобы
какая либо переменная была видна в нескольких функциях, Вы должны объявить ее во всех
функциях как global. Переменные, которые Вы заводите в командном окне Matlab или в скриптах,
которые запускаете из командного окна, являются также локальными. Чтобы сделать переменную
доступной для какой либо функции необходимо объявить ее оператором global. Оператор global
является удобным средством передачи данных между командным окном и функциями или между
функциями.
Функция myfunc возвращает значение функции sin(-alpha*x2)*cos(x).
Причем, как видно из примененных знаков операций (.^ и .*), функция может принимать
в качестве входного параметра x матрицу любого размера и возвращать матрицу y такого же
размера со значениями функции для каждого матричного элемента x.
Чтобы можно было использовать функцию необходимо включить в path путь, где лежит файл
с функцией, либо сделать коталог с этим файлом текущим каталогом. Используем функцию myfunc
в качестве подынтегральной функции для вычисления определенного интеграла в пределах [0 1]
c помощью функции quadl (стандартная функция пакета Matlab для вычисления определенных
интегралов).
cd e:\bvv\matlab %path to myfunc.m
global alpha
alpha=1.5;
s=quadl('myfunc',0,1)
Усложним немного задачу. Пусть требуется построить график функции
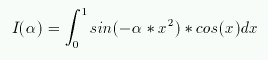 .
Подынтегральная функция определена в файле myfunc.m.
Пример скрипта, решающего поставленную задачу содержится в файле l1_3.m .
clear all %clear memory
global alpha
k=1;
for alpha=1:0.1:4
s(k)=quadl('myfunc',0,1);
a(k)=alpha;
k=k+1;
end
plot(a,s)
В этой программе показано использование оператора цикла for. Чтобы получить полную
информацию о синтаксисе оператора for наберите в коммандном окне help for и получите
полную информацию. Отмечу лишь, что оператор for всегда заканчивается оператором end.
Здесь же хочу отметить еще одну особенность функций в языке Matlab. В отличие от других
языков программирования, функции в Matlab могут возвращать произвольное количество
переменных. Например, [r,c]=size(a);. Функция size возвращает число строк и столбцов
матрицы. Функция eig, вычисляющая собственные вектора и собственные значения,
обсуждалась выше.
Для вычисления детерминанта матрицы можно использовать функцию det,
для суммирования всех элементов вектор-строки или вектор-столбца можно
использовать функцию sum, для того, чтобы получить произведение всех элементов
массива используется функция prod. Это очень простые функции и примеры я не привожу,
а лишь напоминаю о команде help для получения полной информации о любой функции.
Вызываемые из m-файлов функции Matlab запоминает в буфере. Посмотреть
список функций в буфере можно командой inmem. Если Вы внесли исправления в
m-файл на диске, то необходимо (в версиях Matlab более ранних чем 6.5) удалить
функцию из буфера командой clear func_name (func_name - имя функции, удаляемой из буфера),
чтобы изменения вступили в силу.
B Matlab 6.5 я не замечал необходимости в этом.
В этой лекции я дал лишь вводную информацию о функциях Matlab. Более сложные моменты,
такие, как функции с переменным числом аргументов и др., будут рассмотрены в отдельной
лекции.
.
Подынтегральная функция определена в файле myfunc.m.
Пример скрипта, решающего поставленную задачу содержится в файле l1_3.m .
clear all %clear memory
global alpha
k=1;
for alpha=1:0.1:4
s(k)=quadl('myfunc',0,1);
a(k)=alpha;
k=k+1;
end
plot(a,s)
В этой программе показано использование оператора цикла for. Чтобы получить полную
информацию о синтаксисе оператора for наберите в коммандном окне help for и получите
полную информацию. Отмечу лишь, что оператор for всегда заканчивается оператором end.
Здесь же хочу отметить еще одну особенность функций в языке Matlab. В отличие от других
языков программирования, функции в Matlab могут возвращать произвольное количество
переменных. Например, [r,c]=size(a);. Функция size возвращает число строк и столбцов
матрицы. Функция eig, вычисляющая собственные вектора и собственные значения,
обсуждалась выше.
Для вычисления детерминанта матрицы можно использовать функцию det,
для суммирования всех элементов вектор-строки или вектор-столбца можно
использовать функцию sum, для того, чтобы получить произведение всех элементов
массива используется функция prod. Это очень простые функции и примеры я не привожу,
а лишь напоминаю о команде help для получения полной информации о любой функции.
Вызываемые из m-файлов функции Matlab запоминает в буфере. Посмотреть
список функций в буфере можно командой inmem. Если Вы внесли исправления в
m-файл на диске, то необходимо (в версиях Matlab более ранних чем 6.5) удалить
функцию из буфера командой clear func_name (func_name - имя функции, удаляемой из буфера),
чтобы изменения вступили в силу.
B Matlab 6.5 я не замечал необходимости в этом.
В этой лекции я дал лишь вводную информацию о функциях Matlab. Более сложные моменты,
такие, как функции с переменным числом аргументов и др., будут рассмотрены в отдельной
лекции.
Как передать в Matlab данные из других программ
Существует два способа пердать данные из программ, написанных на других языках
программирования, в Matlab.
1. Программа, написанная на любом языке программирования, записывает данные в
текстовый файл на диске. Текст в файле должен иметь форму матрицы с произвольным
числом строк и столбцов. Матричные элементы в файле разделены, как минимум, одним пробелом.
В файле не должно быть символов которые не могут быть интерпретированы как данные.
Если Вы приготовили такой файл, тогда данные из этого файла могут быть загружены
в переменную Matlab. В файле c_to_matlab.c приведен пример
программы, которая пишет 100 строк и 2 столбца в файл res.dat.
#include
#include
double func(double);
void main(void){
FILE *str;
int i;
double x,y,step;
str=fopen("res.dat","w");
for(i=0,step=2*M_PI/100;i<100;i++){x=step*i; y=func(x);
fprintf(str,"%e %e\n",x,y);
}
fclose(str);
}
double func(double t){return sin(t*t)*exp(-t); }
Вот фрагмент файла res.dat, записанного на диск после работы программы.
0.000000e+000 0.000000e+000
6.283185e-002 3.707414e-003
1.256637e-001 1.392601e-002
1.884956e-001 2.942038e-002
2.513274e-001 4.909540e-002
3.141593e-001 7.197088e-002
3.769911e-001 9.715699e-002
4.398230e-001 1.238315e-001
5.026548e-001 1.512199e-001
Предположим, что файл res.dat находится в директории e:\bvv\matlab. Чтобы иметь
возможность загрузить данные из этого файла в Matlab, необходимо включить директорию
e:\bvv\matlab в пути, просматриваемые матлабом. В файле l1_4.m
содержится программа, которая считывет данные из файла res.dat и сохраняет их в
переменной с именем res. Затем строится график функции по данным, хранящимся
в переменной res. Причем считается, что в первом столбце переменной res содержатся
значения независимой переменной, а во втором - значения функции.
clear all % clear of memory
cd e:\bvv\matlab % make current directory e:\bvv\matlab
load res.dat % load data from file res.dat to matlab variable res
plot(res(:,1),res(:,2)); % draw graphik
2. Второй путь организовать взаимодействие между Matlab и программой, написаной на другом
языке программирования, это использование mex-функций. Этот метод позволяет вызвать из
программы, написанной на языке Matlab, программу, написаннную на языках программирования
C, C++ или Fortran. Mex-функции позволяют организовать обмен данными в обоих направлениях
и являются очень мощным инструментом, позволяющим объединить мощь языков С, С++, Fortran
и Matlab в одной программе. Рассмотрению mex-функций будет посвящена отдельная лекция.
О рациональной технике программирования в Matlab
Расмотрим работу функции l1_5, хранящуюся в одноименном файле l1_5.m .
function l1_5()
clear all
tic
x=0:2*pi/10000:2*pi;
y=exp(-x.^2).*cos(x);
toc
tic
for i=1:10001
c(i)=2*pi/10000*(i-1);
d(i)=exp(-x(i)^2)*cos(x(i));
end
toc
Работа этой функции состоит из двух частей. Первая часть начинается с вызова функции tic -
таймера, затем вычисляются значения двух массивов x и y, и вызывается функция toc - вывести
на экран время в секундах, прошедшее с момента включения таймера.
Вторая часть функции начинается вновь с включения таймера. Затем в цикле for вычисляются
значения массивов c и d. Содержимое массивов c,d полностью совпадает с содержимым
массивов x и y. Обе части функции делают практически одно и тоже, но используя
разные операторы. После запуска функции l1_5 на моем компьютере я получил, что время
выполнения первой части 0.01 секунды, а второй - 4.1 секунды. Хорошо известный
в среде программистов на Matlab результат - использование циклов снижает быстродействие
программы более чем на два порядка.
Следующий пример из файла l1_6.m продолжение темы.
clear all
tic
x=rand(10000,1);
s=sum(x);
toc
tic
s=0;
for i=1:10000
c(i)=rand(1);
s=s+c(i);
end
toc
Эта программа тоже состоит из двух частей, проводяших одинаковые вычисления, но разными
средствами. В обоих случаях заводится массив из 10000 случайных чисел и суммируются его
элементы. После выполнения этой прграммы на моем домашнем компьютере я получил, что
первая часть выполняется за 0.01 секунды, вторая - 27 секунд.
Старайтесь свести использование циклов в программах к минимуму. Иногда бывает полезно
делать вставки на С, С++ или Fortran в тех местах программы, где циклы существенно
снижают быстродействие.
Список наиболее часто употребляемых функций пакета Matlab
В этом параграфе приводится список наиболее часто употребляемых функций, входящих
в стандартную поставку пакета. В этот список не включены функции из прикладных
пакетов.
Элементарные функции
abs абсолютное значение и комплексная амплитуда
acos,acosh арккосинус и гиперболический арккосинус
acot,acoth арккотангенс и гиперболический арккотангенс
acsc,acsch арккосеканс и гиперболический арккосеканс
angle фаза комплексного числа в радианах
asec,asech арксеканс и гиперболический арксеканс
asin,asinh арксинус и гиперболический арксинус
atan,atanh арктангенс и гиперболический арктангенс
atan2 арктангенс со значениями из интервала [0 2*pi]
ceil округление вперед
conj комплексное сопряжение
cos,cosh косинус и гиперболический косинус
cot,coth котангенс и гиперболический котангенс
csc,csch косеканс и гиперболический косеканс
exp экспонента
fix округление назад к нулю
floor округление назад к минус бесконечности
gcd наибольший общий делитель
imag мнимая часть комплексного числа
lcm наименьший общий множитель
log натуральный логарифм
log2 логарифм по основанию 2
log10 логарифм по основанию 10
mod знаковый остаток от деления
real вещественная часть комплексного числа
rem остаток от деления
round округление до ближайшего целого
sec,sech секанс и гиперболический секанс
sign знаковая функция
sin,sinh синус и гиперболический синус
sqrt корень квадратный
tan,tanh тангенс и гиперболический тангенс
Специальные функции
airy функции Эйри
besselh функции Ханкеля
besseli,besselk модифицированные функции Бесселя
besselj,bessely функции Бесселя
beta,betainc,betaln бета функции
ellipj эллиптические функции Якоби
ellipke полные эллиптические интегралы первого и второго рода
erf,erfc,erfcx,erfinv функции ошибок
gamma,gammainc,gammaln гамма функции
legendre присоединенные функции Лежандра
Функции для работы с матрицами
cond число обусловленности по отношению к обращению
condeig число обусловленности по отношению к вычислению собственных значений
det детерминант матрицы
norm норма матрицы
rank ранг матрицы
trace след матрицы
\ решение системы линейных уравнений
chol Холецкого факторизация
inv обращение матрицы
lu LU факторизация
qr ортогонально-треугольная декомпозиция
eig собственные вектора и собственные значения
hess Хессенберга форма
qz QZ факторизация обобщенной проблемы собственных значений
schur Шура декомпозиция
Функции для численного анализа
max максимальные элементы массивов
min минимальные элементы массивов
prod произведение элементов массива
sort сортировка
sum суммирование элементов массива
del2 дискретный лапласиан
diff аппроксимация производных
gradient численный градиент
fft одномерное быстрое Фурье преобразование
fft2 двумерное быстрое Фурье преобразование
ifft одномерное обратное быстрое Фурье преобразование
ifft2 двумерное обратное быстрое Фурье преобразование
roots корни полинома
polyfit аппроксимация кривой полиномом
dblquad двойной интеграл
fmin минимум функции одной переменной
fmins минимум функции нескольких переменных
fzero ноль функции одной переменной
ode45,ode23,ode23s,... интегрирование обыкновенных дифференциальных уравнений
quad,quadl,quad8 численное интегрирование
Задачи
1. Написать программу на языке Си для вычисления определенного интеграла методом Симпсона
от функции f(x)=cos(a*x)*sin(3*x) для a=0.1,0.2,0.3,...10. Интеграл вычисляется в пределах
[0 1]. При вычислении использовать библиотеку , разработанную в первом семестре.
Результат счета занести в текстовый файл с двумя колонками для значений параметра a и
интеграла. Загрузить данные из файла в Matlab и построить график зависимости значения
интеграла от параметра а. Проделать те же вычисления, пользуясь исключительно средствами
Matlab, используя функцию матлаба quadl для вычисления определенных интегралов.
Два графика построить в одних координатных осях. Графики рисовать разными цветами и маркерами.
Подписать оси координат, а в поле графиков вывести текст с именем нарисованной функции.
Используя функцию saveas сохранить файл с графиком на диске в формате jpeg.
2. Написать программу, вычисляющую норму вектора произвольной длины. Напишите программу
в двух вариантах - с использованием цикла for и без него. Сравните быстродействие.
В matlab имеется функция norm для вычисления нормы вектора. Сравните быстродействие
своих программ и функции norm.
next home
 Рис. 1.1 Среда разработки Matlab
По умолчанию открыто три окна. Окно Command Window предназначено для ввода команд,
в окне Workspace отображаются переменные , храняшиеся в памяти. Окно Command History
протоколирует вводимые команды. Операторы Matlab могут вводиться в командном окне
или из файлов с именами *.m (звездочка обозначает произвольное имя).
Например, если в директории е:\bvv\matlab имеется файл
name.m c набором операторов Matlab, то для его выполнения необходимо
выполнить следующие действия.
1. Ввести в командном окне Matlab команду path(path,'e:\bvv\matlab'); .
Эта команда добавляет к пути поиска m-файлов путь e:\bvv\matlab.
2. После добавления пути к переменной path можно запускать программу, набрав в командном
окне name (без .m).
При вводе команды name Matlab выполняет следующие действия.
1. Просматривает список переменных в памяти и, если в памяти хранится переменная
с именем name, ее значение выводится на экран.
2. Если переменнная с именем name не найдена, далее просматриваются все файлы в текущей
директории. Текущая директория определена в окне Current Directory среды разработки.
Сменить текущую директорию можно командой cd. Например, cd e:\bvv\matlab. Вывести текущую
директорию на экран можно командой pwd.
Если файл name.m найден, он запускается на выполнение.
3. Если в текущей директории файл name.m не обнаружен, тогда просматриваются все пути
из переменной path и первый найденный файл name.m запускается на выполнение.
Следует обратить особое внимание на имена создаваемых m-файлов. Дело в том, что в Matlab
в директории %MATLAB\toolbox (%MATLAB - путь к директории, где инсталлирован Matlab)
содержится очень большое количество файлов с именами *.m, а пути на все поддиректории
директории toolbox содержатся в переменной path. Команда path(path,'e:\bvv\matlab')
добавляет путь e:\bvv\matlab в конец переменной path, поэтому возникает опасность
дублирования имен, а я уже отмечал, что Matlab запускает на исполнение первый найденный
файл. Можно добавлять свой путь поиска в начало или в конец переменной path командой
addpath. Например, чтобы добавить путь e:\bvv\matlab в начало переменной path нужно
ввести команду addpath e:\bvv\matlab -begin, а команда addpath e:\bvv\matlab -end
поставит этот путь в конец переменной path.
Удалить путь из переменнной path можно командой rmpath e:\bvv\matlab.
В любой момент можноь получить справку о любой функции matlab с помощью команды
help. Например, чтобы получить информацию о синтаксисе команды addpath, необходимо
ввести команду help addpath. Получить список переменных, хранящихся в памяти, позволяет
команда whos (или ее короткая форма who). Удалить переменную var из памяти можно
командой clear var, а удалить все переменные из памяти clear all.
Команда format управляет форматом вывода переменных на консоль.
Рис. 1.1 Среда разработки Matlab
По умолчанию открыто три окна. Окно Command Window предназначено для ввода команд,
в окне Workspace отображаются переменные , храняшиеся в памяти. Окно Command History
протоколирует вводимые команды. Операторы Matlab могут вводиться в командном окне
или из файлов с именами *.m (звездочка обозначает произвольное имя).
Например, если в директории е:\bvv\matlab имеется файл
name.m c набором операторов Matlab, то для его выполнения необходимо
выполнить следующие действия.
1. Ввести в командном окне Matlab команду path(path,'e:\bvv\matlab'); .
Эта команда добавляет к пути поиска m-файлов путь e:\bvv\matlab.
2. После добавления пути к переменной path можно запускать программу, набрав в командном
окне name (без .m).
При вводе команды name Matlab выполняет следующие действия.
1. Просматривает список переменных в памяти и, если в памяти хранится переменная
с именем name, ее значение выводится на экран.
2. Если переменнная с именем name не найдена, далее просматриваются все файлы в текущей
директории. Текущая директория определена в окне Current Directory среды разработки.
Сменить текущую директорию можно командой cd. Например, cd e:\bvv\matlab. Вывести текущую
директорию на экран можно командой pwd.
Если файл name.m найден, он запускается на выполнение.
3. Если в текущей директории файл name.m не обнаружен, тогда просматриваются все пути
из переменной path и первый найденный файл name.m запускается на выполнение.
Следует обратить особое внимание на имена создаваемых m-файлов. Дело в том, что в Matlab
в директории %MATLAB\toolbox (%MATLAB - путь к директории, где инсталлирован Matlab)
содержится очень большое количество файлов с именами *.m, а пути на все поддиректории
директории toolbox содержатся в переменной path. Команда path(path,'e:\bvv\matlab')
добавляет путь e:\bvv\matlab в конец переменной path, поэтому возникает опасность
дублирования имен, а я уже отмечал, что Matlab запускает на исполнение первый найденный
файл. Можно добавлять свой путь поиска в начало или в конец переменной path командой
addpath. Например, чтобы добавить путь e:\bvv\matlab в начало переменной path нужно
ввести команду addpath e:\bvv\matlab -begin, а команда addpath e:\bvv\matlab -end
поставит этот путь в конец переменной path.
Удалить путь из переменнной path можно командой rmpath e:\bvv\matlab.
В любой момент можноь получить справку о любой функции matlab с помощью команды
help. Например, чтобы получить информацию о синтаксисе команды addpath, необходимо
ввести команду help addpath. Получить список переменных, хранящихся в памяти, позволяет
команда whos (или ее короткая форма who). Удалить переменную var из памяти можно
командой clear var, а удалить все переменные из памяти clear all.
Команда format управляет форматом вывода переменных на консоль.
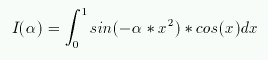 .
Подынтегральная функция определена в файле myfunc.m.
Пример скрипта, решающего поставленную задачу содержится в файле l1_3.m .
clear all %clear memory
global alpha
k=1;
for alpha=1:0.1:4
s(k)=quadl('myfunc',0,1);
a(k)=alpha;
k=k+1;
end
plot(a,s)
В этой программе показано использование оператора цикла for. Чтобы получить полную
информацию о синтаксисе оператора for наберите в коммандном окне help for и получите
полную информацию. Отмечу лишь, что оператор for всегда заканчивается оператором end.
Здесь же хочу отметить еще одну особенность функций в языке Matlab. В отличие от других
языков программирования, функции в Matlab могут возвращать произвольное количество
переменных. Например, [r,c]=size(a);. Функция size возвращает число строк и столбцов
матрицы. Функция eig, вычисляющая собственные вектора и собственные значения,
обсуждалась выше.
Для вычисления детерминанта матрицы можно использовать функцию det,
для суммирования всех элементов вектор-строки или вектор-столбца можно
использовать функцию sum, для того, чтобы получить произведение всех элементов
массива используется функция prod. Это очень простые функции и примеры я не привожу,
а лишь напоминаю о команде help для получения полной информации о любой функции.
Вызываемые из m-файлов функции Matlab запоминает в буфере. Посмотреть
список функций в буфере можно командой inmem. Если Вы внесли исправления в
m-файл на диске, то необходимо (в версиях Matlab более ранних чем 6.5) удалить
функцию из буфера командой clear func_name (func_name - имя функции, удаляемой из буфера),
чтобы изменения вступили в силу.
B Matlab 6.5 я не замечал необходимости в этом.
В этой лекции я дал лишь вводную информацию о функциях Matlab. Более сложные моменты,
такие, как функции с переменным числом аргументов и др., будут рассмотрены в отдельной
лекции.
.
Подынтегральная функция определена в файле myfunc.m.
Пример скрипта, решающего поставленную задачу содержится в файле l1_3.m .
clear all %clear memory
global alpha
k=1;
for alpha=1:0.1:4
s(k)=quadl('myfunc',0,1);
a(k)=alpha;
k=k+1;
end
plot(a,s)
В этой программе показано использование оператора цикла for. Чтобы получить полную
информацию о синтаксисе оператора for наберите в коммандном окне help for и получите
полную информацию. Отмечу лишь, что оператор for всегда заканчивается оператором end.
Здесь же хочу отметить еще одну особенность функций в языке Matlab. В отличие от других
языков программирования, функции в Matlab могут возвращать произвольное количество
переменных. Например, [r,c]=size(a);. Функция size возвращает число строк и столбцов
матрицы. Функция eig, вычисляющая собственные вектора и собственные значения,
обсуждалась выше.
Для вычисления детерминанта матрицы можно использовать функцию det,
для суммирования всех элементов вектор-строки или вектор-столбца можно
использовать функцию sum, для того, чтобы получить произведение всех элементов
массива используется функция prod. Это очень простые функции и примеры я не привожу,
а лишь напоминаю о команде help для получения полной информации о любой функции.
Вызываемые из m-файлов функции Matlab запоминает в буфере. Посмотреть
список функций в буфере можно командой inmem. Если Вы внесли исправления в
m-файл на диске, то необходимо (в версиях Matlab более ранних чем 6.5) удалить
функцию из буфера командой clear func_name (func_name - имя функции, удаляемой из буфера),
чтобы изменения вступили в силу.
B Matlab 6.5 я не замечал необходимости в этом.
В этой лекции я дал лишь вводную информацию о функциях Matlab. Более сложные моменты,
такие, как функции с переменным числом аргументов и др., будут рассмотрены в отдельной
лекции.