Лекция 4. Разработка интерфейсных программ
(продолжение). Символьные вычисления в матлабе
Содержание
Функции uimenu и uicontextmenu
Как работать со слайдерами
Символьные вычисления в матлабе
Задачи
Функции uimenu и uicontextmenu
Функция uimenu создает новое системное меню в текущем графическом окне. Например, оператор
f=uimenu('label','workspace');
создает новое системное меню с именем workspace.
Следующие операторы добавляют три строки к меню workspace и связывают с ними callback-функции.
uimenu(f,'label','figure','callback','myfigure');
uimenu(f,'label','save','callback','mysave');
uimenu(f,'label','Quit','callback','exit','separator','on','Accelerator','Q');
Далее к меню workspace добавляем строку-меню.
f2=uimenu(f,'label','new');
И добавляем новые строки к меню new.
uimenu(f2,'label','up','callback','myup');
uimenu(f2,'label','down','callback','mydown');
На рис.4.1 показано созданное меню.
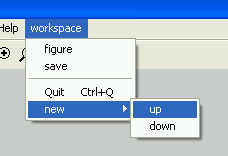Для работы всех пунктов меню необходимо написать все callback функции.
Функция uicontextmenu позволяет создать меню, связанное с любым графическим объектом.
Вызов меню осуществляется нажатием правой кнопки мыши на графическом объекте.
В файле ex_contextmenu.m содержится функция ex_contextmenu,
которая рисует на экране график и связывает с этим графиком всплывающее меню.
Для вызова меню достаточно перевести указатель мыши на нарисованную кривую и
нажать првую кнопку мыши.
function ex_contextmenu()
%clear all
x=1:0.10:10;
y=cos(x.^2).*sin(x.^3);
h=plot(x,y);
c1=uicontextmenu;
it1=uimenu(c1,'label','dashed','callback','set(gco,''linestyle'',''--'')');
it1=uimenu(c1,'label','solid','callback','set(gco,''linestyle'',''-'')');
it1=uimenu(c1,'label','red','callback','set(gco,''color'',[1 0 0])');
set(h,'uicontextmenu',c1);
Результат работы функции ex_contextmenu показан на рис. 4.2.
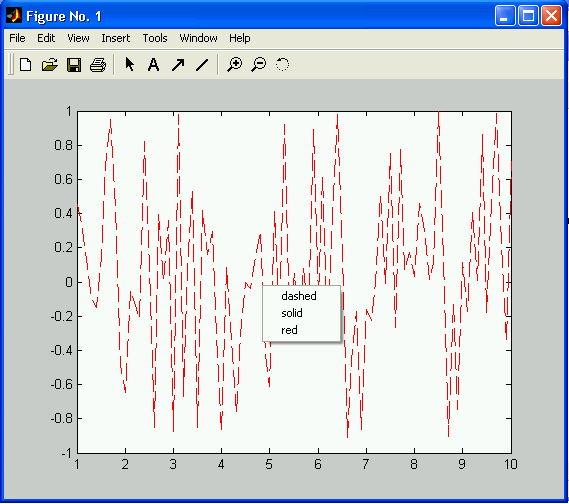Обратите внимание, что в качестве callback-функций используются не имена функций,
а просто команды matlab. Функция gco, использованнная в примере, возвращает указатель
на текущий графический объект ( аббревиатура от трех английских слов get current object).
Как работать со слайдерами
Для работы со слайдерами используется объект типа slider. Следующий оператор открывает
слайдер в текущем графическом окне.
global h
h=uicontrol('style','slider','units','normalized','position',[...],'callback','hsc');
Для обработки событий со слайдером должна быть описана функция hsc, имеющая примерно
такой вид
function hsc()
global h
r=get('h','value');
.
.
.
Задача функции hsc - считать положение слайдера. Каждый объект типа slider имеет поле
value, определяющее положение слайдера. По умолчанию значение этого поля изменяется от
0 (наименьшее положение) до 1 (максимальное положение).
В файле colorrgb.m содержится пример функции с использованием
слайдеров.
function colorrgb()
%#function hsc
global hs1 hs2 hs3 ht1 ht2 ht3 hf
figure(1)
set(gcf,'color',[1 1 0]);
hf=uicontrol('style','frame','backgroundcolor',[0 0 0],'units','normalized',...
'position',[0.5 0.1 0.3 0.3]);
hs1=uicontrol('style','slider','units','normalized','position',...
[0.1 0.1 0.05 0.3],'callback','hsc');
hs2=uicontrol('style','slider','units','normalized','position',...
[0.2 0.1 0.05 0.3],'callback','hsc');
hs3=uicontrol('style','slider','units','normalized','position',...
[0.3 0.1 0.05 0.3],'callback','hsc');
ht1=uicontrol('style','text','units','normalized','position',...
[0.05 0.01 0.1 0.06],'string','0');
ht2=uicontrol('style','text','units','normalized','position',...
[0.16 0.01 0.1 0.06],'string','0');
ht3=uicontrol('style','text','units','normalized','position',...
[0.27 0.01 0.1 0.06],'string','0');
uicontrol('style','pushbutton','units','normalized','position',...
[0.5 0.01 0.3 0.06],'callback','delete(gcf)','string','Cancel');
uicontrol('style','text','units','normalized','position',...
[0.08 0.41 0.08 0.05],'string','Red','backgroundcolor',[1 0 0]);
uicontrol('style','text','units','normalized','position',...
[0.18 0.41 0.08 0.05],'string','Green','backgroundcolor',[0 1 0]);
uicontrol('style','text','units','normalized','position',...
[0.28 0.41 0.08 0.05],'string','Blue','backgroundcolor',[0 0 1]);
Обработку перемещений слайдеров осуществляет функция hsc
hsc.m
function hsc
global hs1 hs2 hs3 ht1 ht2 ht3 hf
r=get(hs1,'value');
g=get(hs2,'value');
b=get(hs3,'value');
set(hf,'backgroundcolor',[r g b]);
set(ht1,'string',num2str(r));
set(ht2,'string',num2str(g));
set(ht3,'string',num2str(b));
Функция colorrgb визуализует результат смешивания трех базовых цветов, интенсивность которых
определяется тремя слайдерами. Результирующий цвет выводится в объекте типа frame, а числовые
значения интенсивностей базовых цветов отображаются объектами типа text. Функция hsc
считывает положения трех слайдеров в переменные r, g и b и назначает цвет фона для объекта
типа frame, ссылка на который хранится в глобальной переменной hf. Значения r,g и b
заносятся в поля объектов типа text, сылки на которые хранятся в глобальных переменных
ht1,ht2 и ht3.
Результат работы функции colorrgb показан на рис. 4.3.
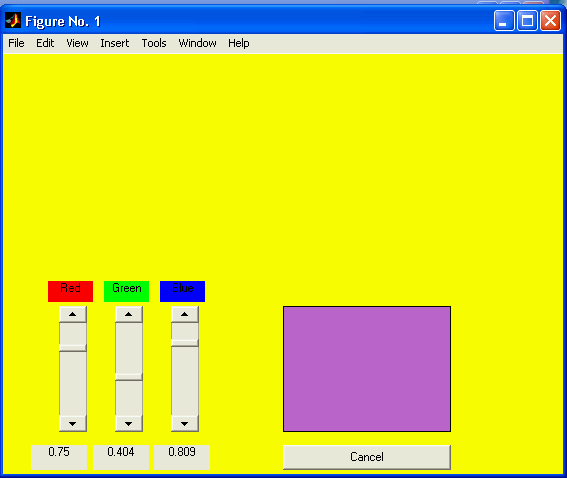
Символьные вычисления в матлабе
Функции для символьных вычислений пакета Matlab реализованы с помощью пакета для символьных
вычислений Maple. Функции для вычисления производных и неопределенных интегралов можно
вызывать используя строковые переменные. Например, следующие три строки вычисляют вторую
производную от функции cos(a*x) по x.
s='cos(a*x)';
s2='x';
s3=diff(s,s2,2);
Для вычисления интеграла исподьзуется функция int.
s4=int(s,s2);
Для вычисления пределов строковых переменных недостаточно, необходимо вводить
символьные переменные. Например, чтобы посчитать предел от sin(x)/x в точке 0
нужно ввести
syms x
s5=limit(sin(x)/x,x,0)
Все функции для символьных переменных возвращают данные типа syms. Этот тип данных
необходимо преобразовывать в строковый при выводе результатов в поля типа string
интерфейсных объектов. Для преобразования используется функция char.
s6=char(s5);
В файле mylimit.m пример интерфейса для вычисления пределов.
function mylimit()
%#function calllim
global fun var point ans
h1=figure;
pos=[0.1 0.7 0.1 0.05];
var=uicontrol('style','edit','units','normalized','position',pos,'string','x');
pos1=[0.1 0.77 0.1 0.05];
point=uicontrol('style','edit','units','normalized','position',pos1,'string','0');
pos2=[0.1 0.84 0.7 0.05];
ans=uicontrol('style','edit','units','normalized','position',pos2);
pos3=[0.01 0.7 0.07 0.05];
uicontrol('style','text','units','normalized','position',pos3,'string','var');
pos4=[0.01 0.77 0.07 0.05];
uicontrol('style','text','units','normalized','position',pos4,'string','point');
pos5=[0.01 0.84 0.07 0.05];
uicontrol('style','text','units','normalized','position',pos5,'string','limit');
pos6=[0.01 0.91 0.07 0.05];
uicontrol('style','pushbutton','units','normalized','position',pos6,...
'string','limit','backgroundcolor',[1 0 0],'callback','calllim');
pos7=[0.3 0.91 0.5 0.05];
fun=uicontrol('style','edit','units','normalized','position',pos7,'string',...
'sin(x)/x');
pos8=[0.2 0.91 0.08 0.05];
uicontrol('style','text','units','normalized','position',pos8,'string','f(t)=');
Callback функция, обрабатывающая нажатие кнопки limit, содержится в файле
calllim.m
function calllim()
global fun var point ans
s1=get(fun,'string');
s2=get(var,'string');
s3=get(point,'string');
s4=sprintf('%s %s','syms',s2);
eval(s4);
s5=strcat('limit(',s1,',',s2,',',s3,')');
s6=eval(s5);
set(ans,'string',char(s6));
Задачи
1. Написать интерфейс для для вычисления производной любого порядка от произвольной функции.
Дифференцируемая функция, переменная по которой производится дифференцирование и порядок
производной вводятся с интерфейса.
2. Написать интерфейс для для вычисления неопределенного интеграла от произвольной функции.
Подынтегральная функция и переменная по которой берется интеграл вводятся с интерфейса.
3. Написать интерфейс для вычисления предела от произвольной функции в заданной точке.
4. Написать интерфейс для разложения произвольной функции в ряд Тейлора в окрестности
заданной точки.
previous next home