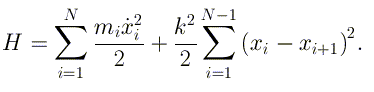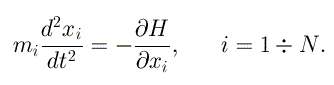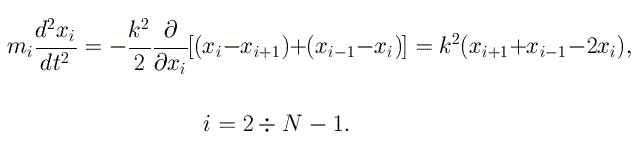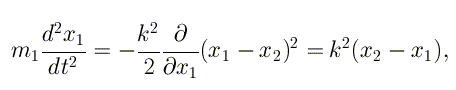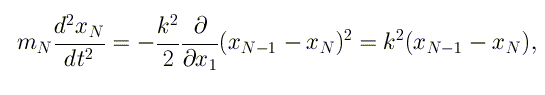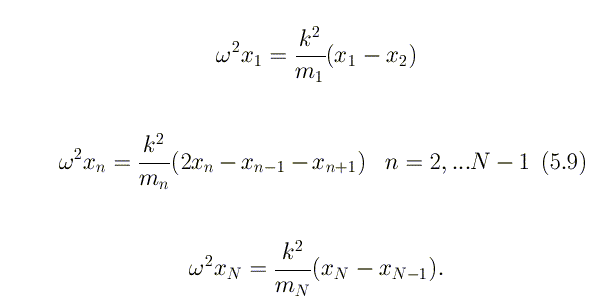Лекция 5. Задачи на собственные значения. Расчет LC-цепи.
Copyright © Красноярский государственный педагогический
университет 2004
Содержание
Решение задачи на собственные значения средствами Matlab.
Расчет LC-цепи.
Задачи
Решение задачи на собственные значения средствами Matlab.
Расчет LC-цепи.
Рассмотрим LC - цепочку , изображенную на рис.1. Отдельное n-ое звено показано на рис.2.
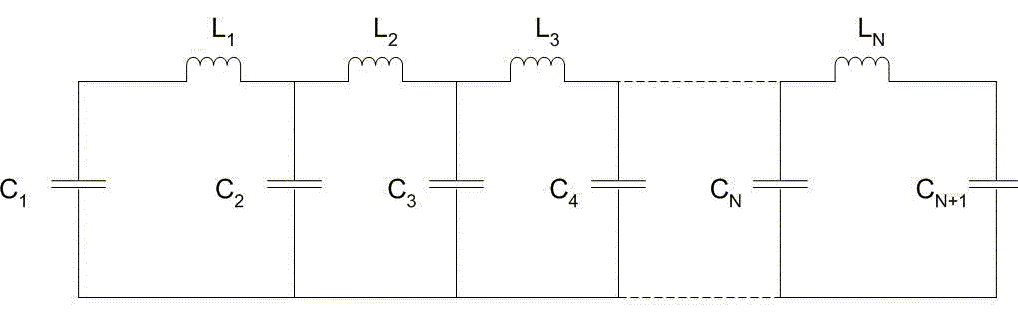 Рис. 1 LC цепь из N ячеек
Рис. 1 LC цепь из N ячеек
 Рис. 2 Отдельная n-ая ячейка LC цепи
На рис. 2 введены обозначения : In - ток , текущий по n - ой индуктивности, Cn - емкость n - го конденсатора, Qn - заряд на обкладках n - го конденсатора,
стрелками показаны положительные направления токов.
Э.д.с. на n-ой индуктивности определяется уравнением 5.1.
Рис. 2 Отдельная n-ая ячейка LC цепи
На рис. 2 введены обозначения : In - ток , текущий по n - ой индуктивности, Cn - емкость n - го конденсатора, Qn - заряд на обкладках n - го конденсатора,
стрелками показаны положительные направления токов.
Э.д.с. на n-ой индуктивности определяется уравнением 5.1.
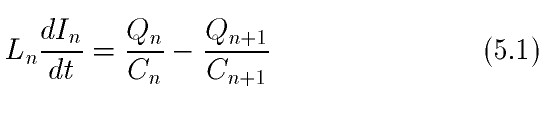 Продифференцировав обе части уравнения 5.1 по времени получим.
Продифференцировав обе части уравнения 5.1 по времени получим.
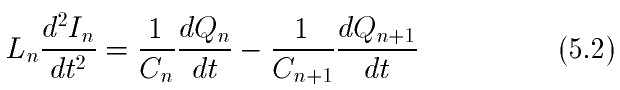 Учитывая, что скорость изменения зарядов на обкладках конденсаторов определяется выра-
жениями 5.3
Учитывая, что скорость изменения зарядов на обкладках конденсаторов определяется выра-
жениями 5.3
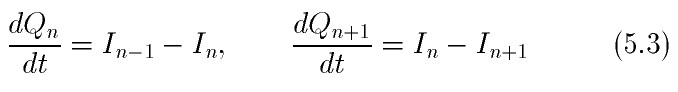 и подставляя это в 5.2 получим:
и подставляя это в 5.2 получим:
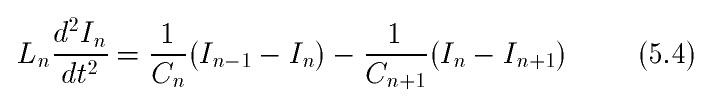 Уравнения 5.4 справедливы для всех n=1,2,...N. Следует учитывать, что для рассматриваемой
цепочки, первая ячейка не имеет левого соседа, а последняя ячейка - правого. Окончательно
уравнения движения для всех ячеек могут быть записаны в виде.
Уравнения 5.4 справедливы для всех n=1,2,...N. Следует учитывать, что для рассматриваемой
цепочки, первая ячейка не имеет левого соседа, а последняя ячейка - правого. Окончательно
уравнения движения для всех ячеек могут быть записаны в виде.
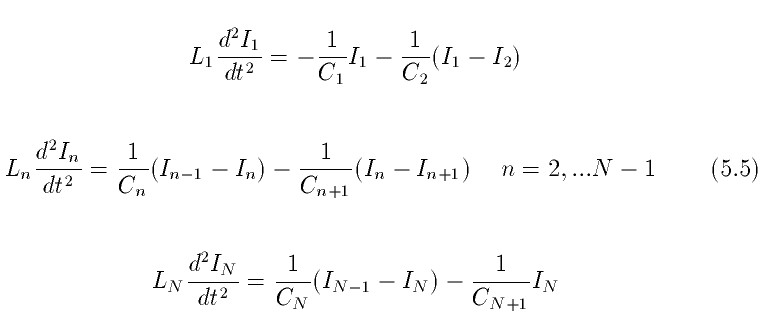 Система уравнений 5.5 представляет полную систему из N уравнений, определяющих
временную эволюцию всех N токов, рассматриваемой LC - цепи. Решения системы
5.5 будем искать в виде:
Система уравнений 5.5 представляет полную систему из N уравнений, определяющих
временную эволюцию всех N токов, рассматриваемой LC - цепи. Решения системы
5.5 будем искать в виде:
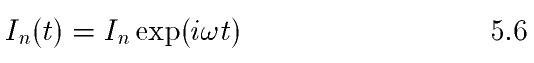 Подставляя 5.6 в 5.5 преобразуем систему дифференциальных уравнений в алгебраическую.
Подставляя 5.6 в 5.5 преобразуем систему дифференциальных уравнений в алгебраическую.
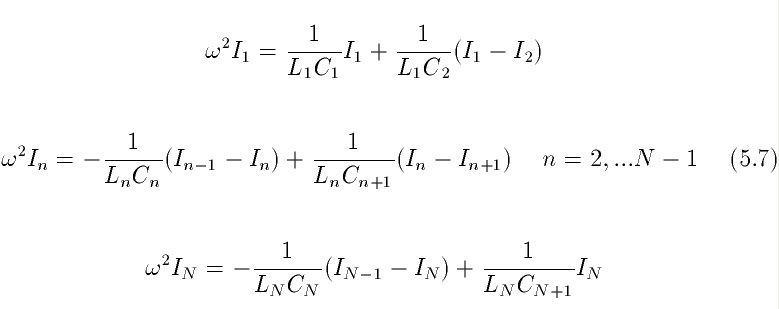 Систему 5.7 можно представить в матричном виде.
Систему 5.7 можно представить в матричном виде.
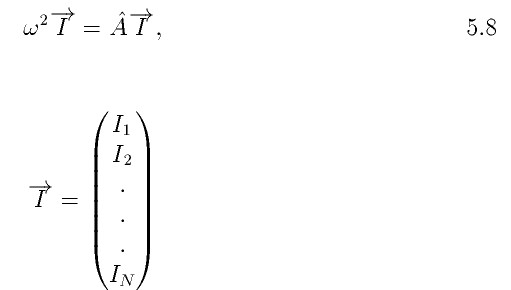 Матрица A имеет вид:
Матрица A имеет вид:
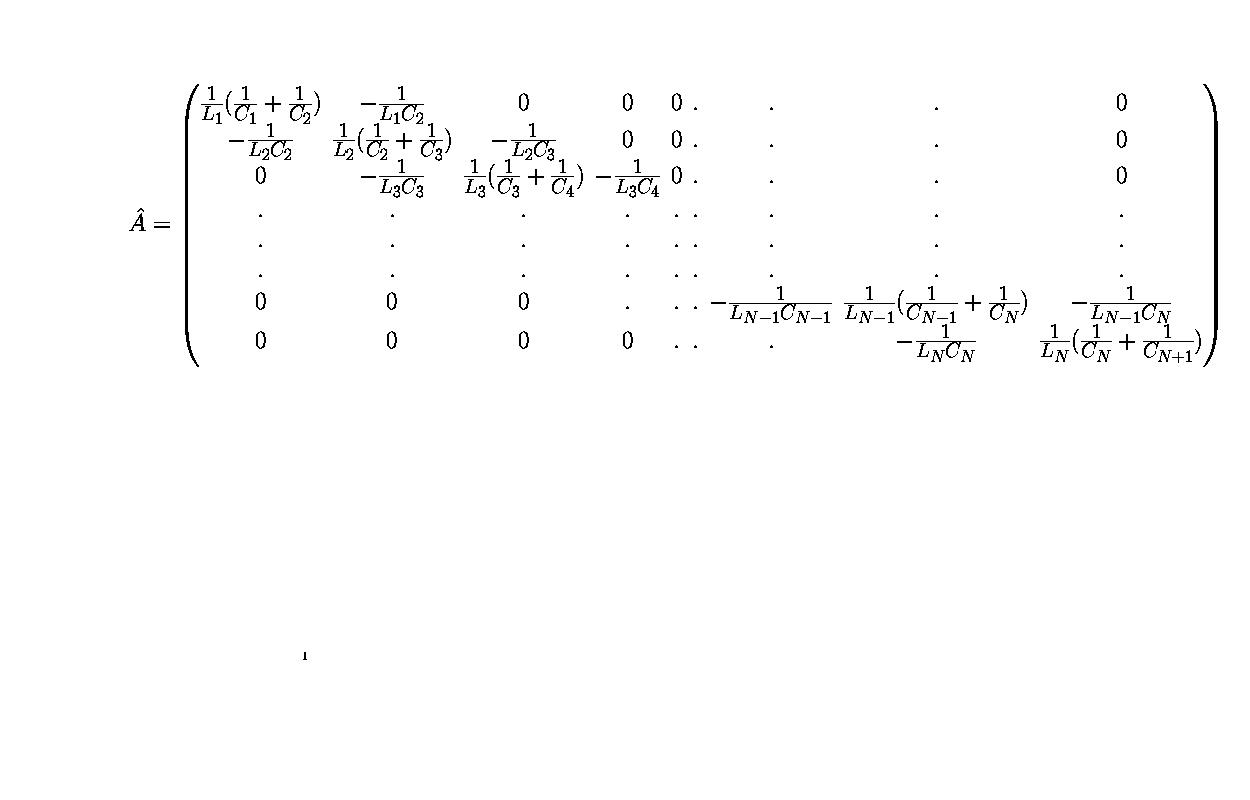 Таким образом решение задачи о колебаниях LC-цепи свелось к решению задачина собственные значения 5.8.
В Матлабе для решения задач на собственные значения применяется функция eig.
Далее приводится пример программы на языке Матлаб для вычисления собственных частот и
соответствующих им форм колебаний цепи произвольной длины.
Программа выводит на экран спектр собственных колебаний, отсортированный
в возрастающем порядке. Затем предлагаетсяв интерактивном режиме с помощью мыши
просмотреть формы колебаний. Необходимое колебание выбирается щелчком левой кнопки
мыши. Заканчивается работа программы при нажатии любой другой кнопки мыши.
clear all
global yy%Ввод числа звеньев LC цепи
N=input('N->');
%tic
L=ones(N,1);
C=ones(N+1,1);
%C(N/2)=1000;
%L(N/2)=1000;%Формирование диагоналей матрицы A
d0=ones(N,1)./L.*(ones(N,1)./C(1:N)+ones(N,1)./C(2:N+1)); % main diagonal of A
d1=-ones(N-1,1)./L(1:N-1).*(ones(N-1,1)./C(2:N)); % upper diagonal
d2=-ones(N-1,1)./L(2:N)./C(2:N); % down diagonal
A=diag(d0,0)+diag(d1,1)+diag(d2,-1);
%toc%вычисление собственных векторов и собственных значений матрицы A
[v,d]=eig(A);
[d1,num]=sort(diag(d)); %to sort diagonal A%интерфейсная часть программы
figure(2);
but=1;
subplot(2,1,1);
plot(d1,'.');
while but==1
[x,y,but]=ginput(1);
xi=round(x);
subplot(2,1,2);
plot(v(:,num(xi)));
subplot(2,1,1);
end
disp('Ok')
Задачи
Таким образом решение задачи о колебаниях LC-цепи свелось к решению задачина собственные значения 5.8.
В Матлабе для решения задач на собственные значения применяется функция eig.
Далее приводится пример программы на языке Матлаб для вычисления собственных частот и
соответствующих им форм колебаний цепи произвольной длины.
Программа выводит на экран спектр собственных колебаний, отсортированный
в возрастающем порядке. Затем предлагаетсяв интерактивном режиме с помощью мыши
просмотреть формы колебаний. Необходимое колебание выбирается щелчком левой кнопки
мыши. Заканчивается работа программы при нажатии любой другой кнопки мыши.
clear all
global yy%Ввод числа звеньев LC цепи
N=input('N->');
%tic
L=ones(N,1);
C=ones(N+1,1);
%C(N/2)=1000;
%L(N/2)=1000;%Формирование диагоналей матрицы A
d0=ones(N,1)./L.*(ones(N,1)./C(1:N)+ones(N,1)./C(2:N+1)); % main diagonal of A
d1=-ones(N-1,1)./L(1:N-1).*(ones(N-1,1)./C(2:N)); % upper diagonal
d2=-ones(N-1,1)./L(2:N)./C(2:N); % down diagonal
A=diag(d0,0)+diag(d1,1)+diag(d2,-1);
%toc%вычисление собственных векторов и собственных значений матрицы A
[v,d]=eig(A);
[d1,num]=sort(diag(d)); %to sort diagonal A%интерфейсная часть программы
figure(2);
but=1;
subplot(2,1,1);
plot(d1,'.');
while but==1
[x,y,but]=ginput(1);
xi=round(x);
subplot(2,1,2);
plot(v(:,num(xi)));
subplot(2,1,1);
end
disp('Ok')
Задачи
1. В приведенном примере программы рассматривается однородная LC
- цепочка.
Все L и C равны
по 1. Изучите как изменятся результаты при введении неоднородности в
цепочку.
2. Решить задачу о колебаниях LC- цепи ,
замкнутой в кольцо. (периодические граничные условия)
3. Рассмотреть собственные колебания
одномерной цепочки гармонически связанных частиц (рис. 3).

Рис. 3 Свободная цепочка гармонически связанных осцилляторов.
В равовесном состоянии все частицы находятся на расстоянии a
друг от друга. При отклонении любой из частиц
от положения равновесия энергия цепочки повышается и в
системе возникают колебания. Если ввести обозначение
xi для смещения i-ой
частицы из положения равновесия, то полная энергия для свободной
цепочки может быть записана
в следующем виде
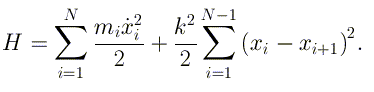
В этом выражении через m i обозначена
масса i-ой частицы, k -
коэффициент упругости.
Уравнения движения для каждой частицы имеют вид
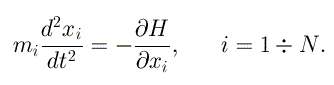
Поскольку каждая внутрення частица цепочки взаимодействует с двумя
соседями, уравнения движения для таких частиц будут
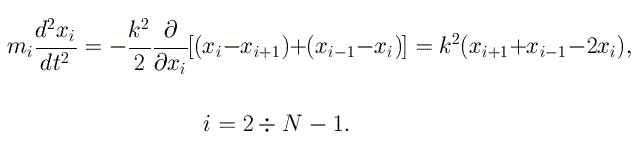
Для первой и последней частиц цепочки уравнения движения будут
такими
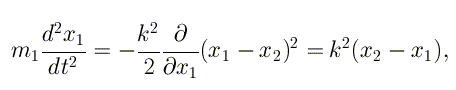
для первой частицы, и
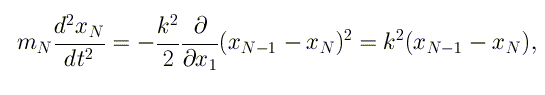
для последней. Искать решения уравнений движения будем в виде xk
(t)=xkexp(iwt),
k=1,2...N.
Подставляя это в уравнения движения
для всех частиц, получим
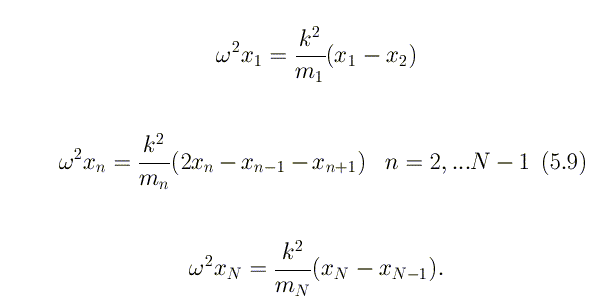
Дальнейший ход решения задачи полностью аналогичен лекции после
формулы (5.8). Студентам предлагается самостоятельно написать
программу для интерактиного исследовани собственных частот и форм
колебаний для случая однородной цепочки, т.е. когда все
массы частиц одинаковы и для простоты равны единице. Коэффициент k
также положить равным единице. Как объяснить
наличие нулевой частоты в спектре колебаний?
Исследовать как изменятся решения когда массы частиц будут
различными.
3.1 Исследовать собственные колебания
цепочки с фиксированными граничными условиями (Рис. 4)

Рис. 4 Цепочка с фиксированными граничными условиями.
В этом случае нулевая и (N+1) частицы
считаются жестко закрепленными в пространстве, колебания могут
совершать лишь
внутренние частицы цепочки с номерами от 1 до N.
Какие характерные изменения в спектре колебаний ?
3.2 Исследовать собственные колебания
цепочки с периодическими граничными условиями, моделирующими
бесконечный кристалл (Рис. 5).

Рис. 5 Цепочка с периодическими граничными условиями.
Эту цепоку удобно представлять, как цепочку из N
частиц, замкнутых в кольцо. Следом за последней N-ой
частицей идет 1-ая частица, а
перед первой частицей находится N-ая
чатица. Изучить особенности спектра собственных колебаний в этом
случае.
previous next home
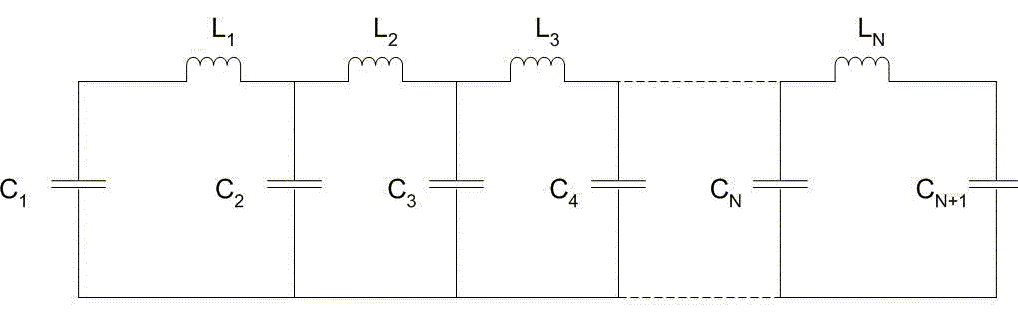 Рис. 1 LC цепь из N ячеек
Рис. 1 LC цепь из N ячеек
 Рис. 2 Отдельная n-ая ячейка LC цепи
На рис. 2 введены обозначения : In - ток , текущий по n - ой индуктивности, Cn - емкость n - го конденсатора, Qn - заряд на обкладках n - го конденсатора,
стрелками показаны положительные направления токов.
Э.д.с. на n-ой индуктивности определяется уравнением 5.1.
Рис. 2 Отдельная n-ая ячейка LC цепи
На рис. 2 введены обозначения : In - ток , текущий по n - ой индуктивности, Cn - емкость n - го конденсатора, Qn - заряд на обкладках n - го конденсатора,
стрелками показаны положительные направления токов.
Э.д.с. на n-ой индуктивности определяется уравнением 5.1.
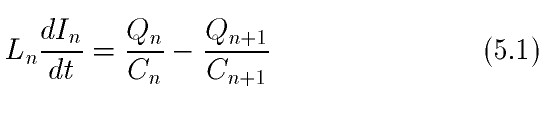 Продифференцировав обе части уравнения 5.1 по времени получим.
Продифференцировав обе части уравнения 5.1 по времени получим.
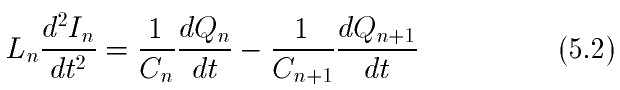 Учитывая, что скорость изменения зарядов на обкладках конденсаторов определяется выра-
жениями 5.3
Учитывая, что скорость изменения зарядов на обкладках конденсаторов определяется выра-
жениями 5.3
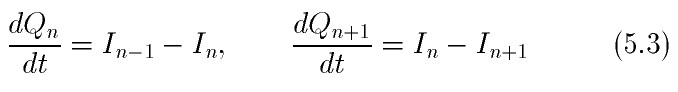 и подставляя это в 5.2 получим:
и подставляя это в 5.2 получим:
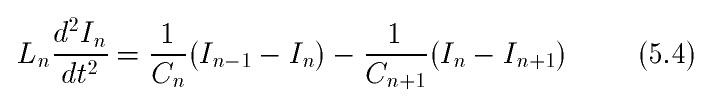 Уравнения 5.4 справедливы для всех n=1,2,...N. Следует учитывать, что для рассматриваемой
цепочки, первая ячейка не имеет левого соседа, а последняя ячейка - правого. Окончательно
уравнения движения для всех ячеек могут быть записаны в виде.
Уравнения 5.4 справедливы для всех n=1,2,...N. Следует учитывать, что для рассматриваемой
цепочки, первая ячейка не имеет левого соседа, а последняя ячейка - правого. Окончательно
уравнения движения для всех ячеек могут быть записаны в виде.
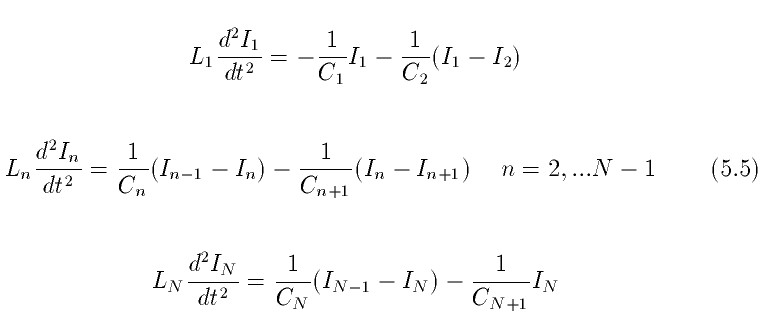 Система уравнений 5.5 представляет полную систему из N уравнений, определяющих
временную эволюцию всех N токов, рассматриваемой LC - цепи. Решения системы
5.5 будем искать в виде:
Система уравнений 5.5 представляет полную систему из N уравнений, определяющих
временную эволюцию всех N токов, рассматриваемой LC - цепи. Решения системы
5.5 будем искать в виде:
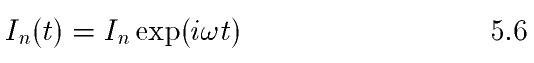 Подставляя 5.6 в 5.5 преобразуем систему дифференциальных уравнений в алгебраическую.
Подставляя 5.6 в 5.5 преобразуем систему дифференциальных уравнений в алгебраическую.
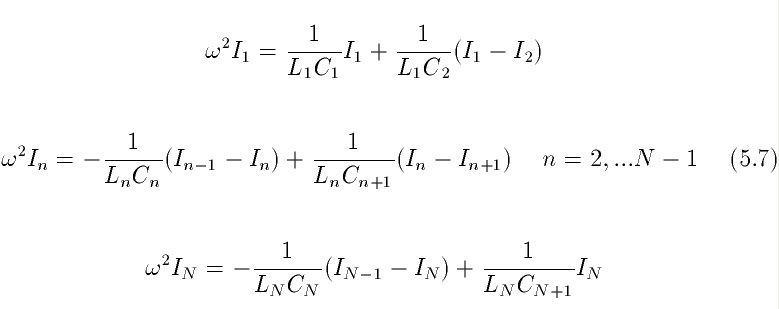 Систему 5.7 можно представить в матричном виде.
Систему 5.7 можно представить в матричном виде.
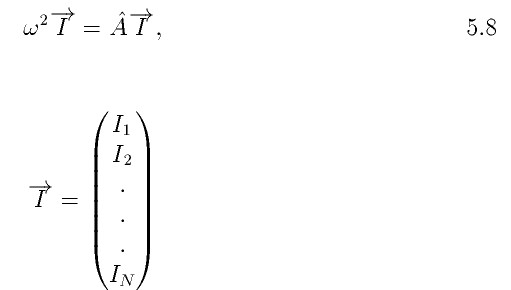 Матрица A имеет вид:
Матрица A имеет вид:
 Таким образом решение задачи о колебаниях LC-цепи свелось к решению задачина собственные значения 5.8.
В Матлабе для решения задач на собственные значения применяется функция eig.
Далее приводится пример программы на языке Матлаб для вычисления собственных частот и
соответствующих им форм колебаний цепи произвольной длины.
Программа выводит на экран спектр собственных колебаний, отсортированный
в возрастающем порядке. Затем предлагаетсяв интерактивном режиме с помощью мыши
просмотреть формы колебаний. Необходимое колебание выбирается щелчком левой кнопки
мыши. Заканчивается работа программы при нажатии любой другой кнопки мыши.
clear all
global yy%Ввод числа звеньев LC цепи
N=input('N->');
%tic
L=ones(N,1);
C=ones(N+1,1);
%C(N/2)=1000;
%L(N/2)=1000;%Формирование диагоналей матрицы A
d0=ones(N,1)./L.*(ones(N,1)./C(1:N)+ones(N,1)./C(2:N+1)); % main diagonal of A
d1=-ones(N-1,1)./L(1:N-1).*(ones(N-1,1)./C(2:N)); % upper diagonal
d2=-ones(N-1,1)./L(2:N)./C(2:N); % down diagonal
A=diag(d0,0)+diag(d1,1)+diag(d2,-1);
%toc%вычисление собственных векторов и собственных значений матрицы A
[v,d]=eig(A);
[d1,num]=sort(diag(d)); %to sort diagonal A%интерфейсная часть программы
figure(2);
but=1;
subplot(2,1,1);
plot(d1,'.');
while but==1
[x,y,but]=ginput(1);
xi=round(x);
subplot(2,1,2);
plot(v(:,num(xi)));
subplot(2,1,1);
end
disp('Ok')
Задачи
Таким образом решение задачи о колебаниях LC-цепи свелось к решению задачина собственные значения 5.8.
В Матлабе для решения задач на собственные значения применяется функция eig.
Далее приводится пример программы на языке Матлаб для вычисления собственных частот и
соответствующих им форм колебаний цепи произвольной длины.
Программа выводит на экран спектр собственных колебаний, отсортированный
в возрастающем порядке. Затем предлагаетсяв интерактивном режиме с помощью мыши
просмотреть формы колебаний. Необходимое колебание выбирается щелчком левой кнопки
мыши. Заканчивается работа программы при нажатии любой другой кнопки мыши.
clear all
global yy%Ввод числа звеньев LC цепи
N=input('N->');
%tic
L=ones(N,1);
C=ones(N+1,1);
%C(N/2)=1000;
%L(N/2)=1000;%Формирование диагоналей матрицы A
d0=ones(N,1)./L.*(ones(N,1)./C(1:N)+ones(N,1)./C(2:N+1)); % main diagonal of A
d1=-ones(N-1,1)./L(1:N-1).*(ones(N-1,1)./C(2:N)); % upper diagonal
d2=-ones(N-1,1)./L(2:N)./C(2:N); % down diagonal
A=diag(d0,0)+diag(d1,1)+diag(d2,-1);
%toc%вычисление собственных векторов и собственных значений матрицы A
[v,d]=eig(A);
[d1,num]=sort(diag(d)); %to sort diagonal A%интерфейсная часть программы
figure(2);
but=1;
subplot(2,1,1);
plot(d1,'.');
while but==1
[x,y,but]=ginput(1);
xi=round(x);
subplot(2,1,2);
plot(v(:,num(xi)));
subplot(2,1,1);
end
disp('Ok')
Задачи