Лекция 7. Интегрирование дифференциальных уравнений и систем
Copyright © Красноярский государственный университет 2003
Содержание
Интегрирование одиночных дифференциальных уравнений
Интегрирование дифференциальных уравнений порядка выше первого и систем
Задачи
Интегрирование одиночных дифференциальных уравнений
Для интегрирования дифференциальных уравнений в Matlab предусмотрены функции
ode45,ode23, ode113, ode15s, ode23s, ode23t, ode23tb. Функции ode23,ode45 и ode113 предназначены
для решения нежестких дифференциальных уравнений и систем. Все остальные функции предназначены
для численного интегрирования жестких дифференциальных уравнений и систем.
Рассмотрим для примера использование функции ode45 для интегрирования одного дифференциального
уравнения dy/dx=x*y c начальным условием y(x0)=1.2. Решение требуется найти
на интервале от x=x0=0.1 до x=xend=2.
Для решения дифференциального уравнения требуется написать функцию, определяющую правую
часть уравнения. Функция, определяющая правую часть нашего дифференциального уравнения
имеет вид (файл ode1.m :
function f=ode1(x,y)
f=x.*y;
Файл ode1.m должен находится в рабочих путях матлаба. Теперь, используя функцию ode1,
интегрируем дифференциальное уравнение (файл solve1.m)
clear all
x0=0.1;
xend=2;
xf=[x0 xend];
y0=1.2;
[x y]=ode45('ode1',xf,y0);
plot(x,y);
Функция ode45 по умолчанию интегрирует с абсолютной погрешностью 0.1*10-6 и
с относительной погрешностью 0.1*10-3. Если вы желаете изменить эти
значения необходимо использовать функцию odeset для заполнения полей структуры, которая
затем будет передана функции ode45 при вызове. Например,
opt=odeset('reltol',1e-4,'abstol',1e-7);
[x y]=ode45('ode1',xf,y0,opt);.
Поле reltol сруктуры opt задает относительную погрешность интегрирования, а поле abstol -
абсолютную погрешность. Функция ode45 сама выбирает значения независимой переменной x
в которых вычисляются значения функции y. Если требуется знать решения y(x) в определенных
точках x необходимо эти точки включить в входной вектор xf. Например, xf=0.1:0.2:2;.
Интегрирование дифференциальных уравнений порядка выше первого и систем
Интегрирование дифференциальног уравнения поряда выше первого всегда можно свести
к интегрированию системы дифференциальных уравнений первого порядка. Например, требуется
проинтегрировать дифференциальное уравнение второго порядка.
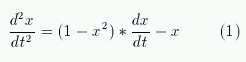 Вводя новые переменные y1=dx/dt и y2=x, приводим уравнение (1)
к системе уравнений первого порядка.
Вводя новые переменные y1=dx/dt и y2=x, приводим уравнение (1)
к системе уравнений первого порядка.
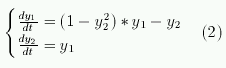 Если ввести в рассмотрение вектора
Если ввести в рассмотрение вектора
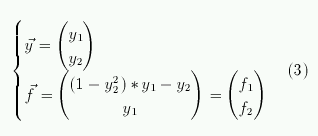 ,
тогда система уравнений (2) может быть записана в векторном виде:
,
тогда система уравнений (2) может быть записана в векторном виде:
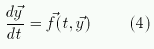 .
Для решения системы уравнений (2)или (4) используем снова функцию ode45.
Вы должны помнить, что функции матлаба одинаково хорошо работают со скалярными и матричными
переменными, поскольку по определению все переменные матлаба являются матрицами.
Прежде всего необходимо написать функцию, определяющую правую часть системы (4)
(файл ode2.m ).
function f=ode2(t,y)
f1=(1-y(2).^2).*y(1)-y(2); % первое уравнение
f2=y(1); %второе уравнение
f=[f1;f2]; % возвращаемый вектор
Теперь можно приступить к интегрированию системы (4) (файл solve2.m ).
clear all
tf=0:0.1:100;
y0=[0.1 0.2];
opt=odeset('reltol',1e-4,'abstol',1e-7);
[t y]=ode45('ode2',tf,y0,opt);
figure(1)
plot(t,y(:,1)); %рисуем график y1(t)
figure(2)
plot(t,y(:,2)); %рисуем график y2(t)
figure(3)
plot(y(:,2),y(:,1),'.'); %рисуем фазовую траекторию y1(y2)
.
Для решения системы уравнений (2)или (4) используем снова функцию ode45.
Вы должны помнить, что функции матлаба одинаково хорошо работают со скалярными и матричными
переменными, поскольку по определению все переменные матлаба являются матрицами.
Прежде всего необходимо написать функцию, определяющую правую часть системы (4)
(файл ode2.m ).
function f=ode2(t,y)
f1=(1-y(2).^2).*y(1)-y(2); % первое уравнение
f2=y(1); %второе уравнение
f=[f1;f2]; % возвращаемый вектор
Теперь можно приступить к интегрированию системы (4) (файл solve2.m ).
clear all
tf=0:0.1:100;
y0=[0.1 0.2];
opt=odeset('reltol',1e-4,'abstol',1e-7);
[t y]=ode45('ode2',tf,y0,opt);
figure(1)
plot(t,y(:,1)); %рисуем график y1(t)
figure(2)
plot(t,y(:,2)); %рисуем график y2(t)
figure(3)
plot(y(:,2),y(:,1),'.'); %рисуем фазовую траекторию y1(y2)
Задачи
Задача. Исследовать фазовую плоскость (несколько фазовых траекторий, построенных при различных
начальных условиях) для одномерной частицы движущейся в потенциале
V(x)=x4-x2. Массу частицы считать равной единице.
Точность решения проверять по сохранению интеграла энергии.
previous next home
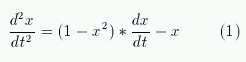 Вводя новые переменные y1=dx/dt и y2=x, приводим уравнение (1)
к системе уравнений первого порядка.
Вводя новые переменные y1=dx/dt и y2=x, приводим уравнение (1)
к системе уравнений первого порядка.
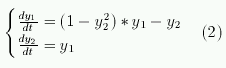 Если ввести в рассмотрение вектора
Если ввести в рассмотрение вектора
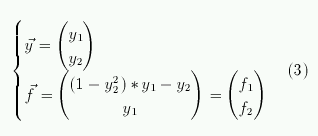 ,
тогда система уравнений (2) может быть записана в векторном виде:
,
тогда система уравнений (2) может быть записана в векторном виде:
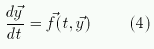 .
Для решения системы уравнений (2)или (4) используем снова функцию ode45.
Вы должны помнить, что функции матлаба одинаково хорошо работают со скалярными и матричными
переменными, поскольку по определению все переменные матлаба являются матрицами.
Прежде всего необходимо написать функцию, определяющую правую часть системы (4)
(файл ode2.m ).
function f=ode2(t,y)
f1=(1-y(2).^2).*y(1)-y(2); % первое уравнение
f2=y(1); %второе уравнение
f=[f1;f2]; % возвращаемый вектор
Теперь можно приступить к интегрированию системы (4) (файл solve2.m ).
clear all
tf=0:0.1:100;
y0=[0.1 0.2];
opt=odeset('reltol',1e-4,'abstol',1e-7);
[t y]=ode45('ode2',tf,y0,opt);
figure(1)
plot(t,y(:,1)); %рисуем график y1(t)
figure(2)
plot(t,y(:,2)); %рисуем график y2(t)
figure(3)
plot(y(:,2),y(:,1),'.'); %рисуем фазовую траекторию y1(y2)
.
Для решения системы уравнений (2)или (4) используем снова функцию ode45.
Вы должны помнить, что функции матлаба одинаково хорошо работают со скалярными и матричными
переменными, поскольку по определению все переменные матлаба являются матрицами.
Прежде всего необходимо написать функцию, определяющую правую часть системы (4)
(файл ode2.m ).
function f=ode2(t,y)
f1=(1-y(2).^2).*y(1)-y(2); % первое уравнение
f2=y(1); %второе уравнение
f=[f1;f2]; % возвращаемый вектор
Теперь можно приступить к интегрированию системы (4) (файл solve2.m ).
clear all
tf=0:0.1:100;
y0=[0.1 0.2];
opt=odeset('reltol',1e-4,'abstol',1e-7);
[t y]=ode45('ode2',tf,y0,opt);
figure(1)
plot(t,y(:,1)); %рисуем график y1(t)
figure(2)
plot(t,y(:,2)); %рисуем график y2(t)
figure(3)
plot(y(:,2),y(:,1),'.'); %рисуем фазовую траекторию y1(y2)