Лекция 6. Вычисление спектров Фурье
Copyright © Красноярский государственный университет 2003
Содержание
Дискретное преобразование Фурье
Задачи
Дискретное преобразование Фурье
Любая периодическая с периодом T функция f(t) может быть разложена в ряд Фурье вида:
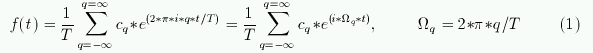 .
Отличные от нуля коэффициенты cq определяют спектр сигнала. Основная задача
Фурье анализа сотоит в вычислении полного набора коэффициентов {cq}.
Предположим, что сигнал f(t) измеряется через интервал
.
Отличные от нуля коэффициенты cq определяют спектр сигнала. Основная задача
Фурье анализа сотоит в вычислении полного набора коэффициентов {cq}.
Предположим, что сигнал f(t) измеряется через интервал 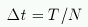 в моменты tl=l*T/N для l=1,2,...N. Тогда для моментов времени t=tl
выражение (1) может быть записано в виде:
в моменты tl=l*T/N для l=1,2,...N. Тогда для моментов времени t=tl
выражение (1) может быть записано в виде:
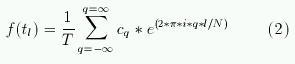 .
После простейших преобразований (2) можно привести к виду:
.
После простейших преобразований (2) можно привести к виду:
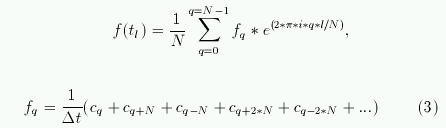 .
Формула (3) определяет дискретное преобразование Фурье для сигнала, заданого значениями
f(t1),f(t2),...f(tN).
Если сигнал f(t) вещественный, то он может быть представлен в форме ряда по синусам и
косинусам:
.
Формула (3) определяет дискретное преобразование Фурье для сигнала, заданого значениями
f(t1),f(t2),...f(tN).
Если сигнал f(t) вещественный, то он может быть представлен в форме ряда по синусам и
косинусам:
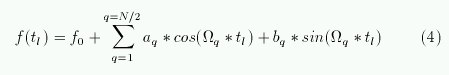 .
Связь между коэффициентами fq и aq, bq определяется
формулами (5).
.
Связь между коэффициентами fq и aq, bq определяется
формулами (5).
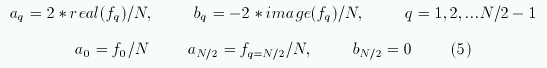 .
В матлабе встроена функция fft, которая вычисляет коэффициенты Фурье разложения fq
по значениям f(t1),f(t2),...f(tN), как это определено
в выражении (3). Для быстрой работы функции fft требуется, чтобы размер входного вектора
f был 2m, где m - любое. После вызова fq=fft(f), в массиве fq хранятся значения
fq для q=0,1,2,...N-1. В первом элементе массива fq(1) содержится значение fq
для q=0 и т.д. Если при некотором значении q величина fq отлична от нуля, то это
означает что в сигнале присутствует гармоника с частотой
.
В матлабе встроена функция fft, которая вычисляет коэффициенты Фурье разложения fq
по значениям f(t1),f(t2),...f(tN), как это определено
в выражении (3). Для быстрой работы функции fft требуется, чтобы размер входного вектора
f был 2m, где m - любое. После вызова fq=fft(f), в массиве fq хранятся значения
fq для q=0,1,2,...N-1. В первом элементе массива fq(1) содержится значение fq
для q=0 и т.д. Если при некотором значении q величина fq отлична от нуля, то это
означает что в сигнале присутствует гармоника с частотой 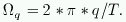 В файле spectr.m содержится функция, которая вычисляет спектр Фурье
{aq,bq} для вещественного сигнала f.
function [a,b,om]=spectr(f,T,N)
s=size(f);
N1=max(s);
if N1~=N
error('size of first argument for spectr must be equals to third argument');
end
N2=min(s);
if N2 ~= 1
error('first argument must be one-dimensional for spectr');
end
p=log(N)/log(2);
if abs(p-round(p))>eps
error('N must be pow of 2 for function spectr');
end
fq=fft(f);
q=0:N/2;
a(1)=fq(1)/N;
a(N/2+1)=fq(N/2+1)/N;
a(2:N/2)=2*real(fq(2:N/2))/N;
b(1)=0;
b(2:N/2)=-2*imag(fq(2:N/2))/N;
b(N/2+1)=0;
om=q/T;
Входные параметры:
f - вектор размера N, содержащий значения сигнала измеренные в моменты времени tl=l*T/N.
T - время, в течении которого проводилось измерение сигнала.
N - размерность вектора f. N должно быть 2m, где m - любое.
Выходные параметры:
a и b - массивы размерности N/2+1, содержащие коэффициенты aq и bq,
как они определены в (4). Для упрощения длина массива b сделана такой же, как и длина
массива a путем добавления в массив b двух элементов b(1)=b(N/2+1)=0. Элемент
массива b(2) соответствует q=1.
om - массив размера N/2+1, содержащий значения частот
В файле spectr.m содержится функция, которая вычисляет спектр Фурье
{aq,bq} для вещественного сигнала f.
function [a,b,om]=spectr(f,T,N)
s=size(f);
N1=max(s);
if N1~=N
error('size of first argument for spectr must be equals to third argument');
end
N2=min(s);
if N2 ~= 1
error('first argument must be one-dimensional for spectr');
end
p=log(N)/log(2);
if abs(p-round(p))>eps
error('N must be pow of 2 for function spectr');
end
fq=fft(f);
q=0:N/2;
a(1)=fq(1)/N;
a(N/2+1)=fq(N/2+1)/N;
a(2:N/2)=2*real(fq(2:N/2))/N;
b(1)=0;
b(2:N/2)=-2*imag(fq(2:N/2))/N;
b(N/2+1)=0;
om=q/T;
Входные параметры:
f - вектор размера N, содержащий значения сигнала измеренные в моменты времени tl=l*T/N.
T - время, в течении которого проводилось измерение сигнала.
N - размерность вектора f. N должно быть 2m, где m - любое.
Выходные параметры:
a и b - массивы размерности N/2+1, содержащие коэффициенты aq и bq,
как они определены в (4). Для упрощения длина массива b сделана такой же, как и длина
массива a путем добавления в массив b двух элементов b(1)=b(N/2+1)=0. Элемент
массива b(2) соответствует q=1.
om - массив размера N/2+1, содержащий значения частот 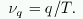 .
.
Задачи
Задача 1. Написать интерфейсную программу для вычисления спектра сигнала. Сигнал,
измеренный в дискретные моменты времени хранится в текстовом файле на диске.
Название файла, значения T и N должны вводиться с интерфейса.
Задача 2. Написать интерфейсную программу для вычисления спектра сигнала. Сигнал
в аналитической форме вводится с интерфейса.
Значения T и N должны также вводиться с интерфейса.
previous next home
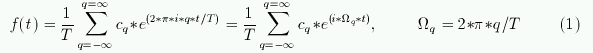 .
Отличные от нуля коэффициенты cq определяют спектр сигнала. Основная задача
Фурье анализа сотоит в вычислении полного набора коэффициентов {cq}.
Предположим, что сигнал f(t) измеряется через интервал
.
Отличные от нуля коэффициенты cq определяют спектр сигнала. Основная задача
Фурье анализа сотоит в вычислении полного набора коэффициентов {cq}.
Предположим, что сигнал f(t) измеряется через интервал 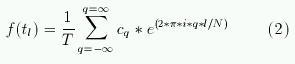 .
После простейших преобразований (2) можно привести к виду:
.
После простейших преобразований (2) можно привести к виду:
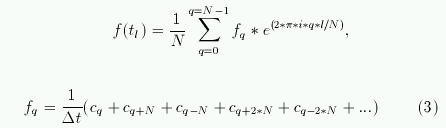 .
Формула (3) определяет дискретное преобразование Фурье для сигнала, заданого значениями
f(t1),f(t2),...f(tN).
Если сигнал f(t) вещественный, то он может быть представлен в форме ряда по синусам и
косинусам:
.
Формула (3) определяет дискретное преобразование Фурье для сигнала, заданого значениями
f(t1),f(t2),...f(tN).
Если сигнал f(t) вещественный, то он может быть представлен в форме ряда по синусам и
косинусам:
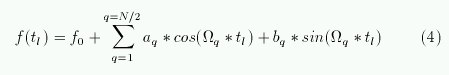 .
Связь между коэффициентами fq и aq, bq определяется
формулами (5).
.
Связь между коэффициентами fq и aq, bq определяется
формулами (5).
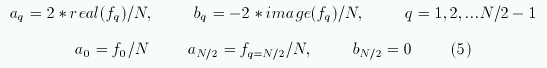 .
В матлабе встроена функция fft, которая вычисляет коэффициенты Фурье разложения fq
по значениям f(t1),f(t2),...f(tN), как это определено
в выражении (3). Для быстрой работы функции fft требуется, чтобы размер входного вектора
f был 2m, где m - любое. После вызова fq=fft(f), в массиве fq хранятся значения
fq для q=0,1,2,...N-1. В первом элементе массива fq(1) содержится значение fq
для q=0 и т.д. Если при некотором значении q величина fq отлична от нуля, то это
означает что в сигнале присутствует гармоника с частотой
.
В матлабе встроена функция fft, которая вычисляет коэффициенты Фурье разложения fq
по значениям f(t1),f(t2),...f(tN), как это определено
в выражении (3). Для быстрой работы функции fft требуется, чтобы размер входного вектора
f был 2m, где m - любое. После вызова fq=fft(f), в массиве fq хранятся значения
fq для q=0,1,2,...N-1. В первом элементе массива fq(1) содержится значение fq
для q=0 и т.д. Если при некотором значении q величина fq отлична от нуля, то это
означает что в сигнале присутствует гармоника с частотой